LeetCode 1971 Find if Path Exists in Graph
Problem description:
There is a bi-directional graph with n vertices, where each vertex is labeled from 0to n - 1
(inclusive). The edges in the graph are represented as 2D integer array edges, where each
edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi.
Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
You want to determine if there is a valid path that exists from vertex source to vertex
destination.
Given edgesand the integers n, source, and destination, return true if there is a valid path from source to destination or falseotherwise.
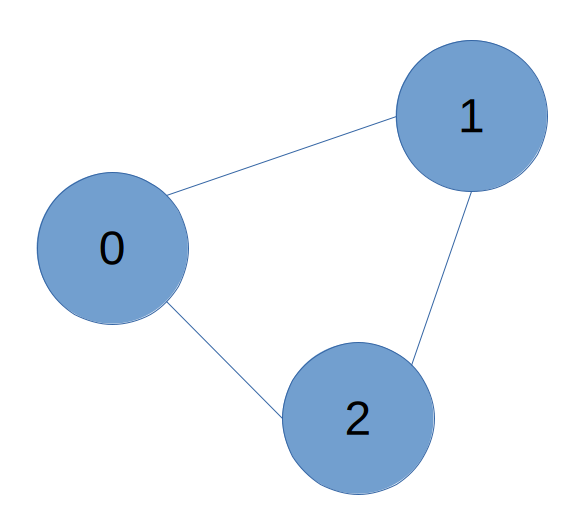
Example 1:
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2
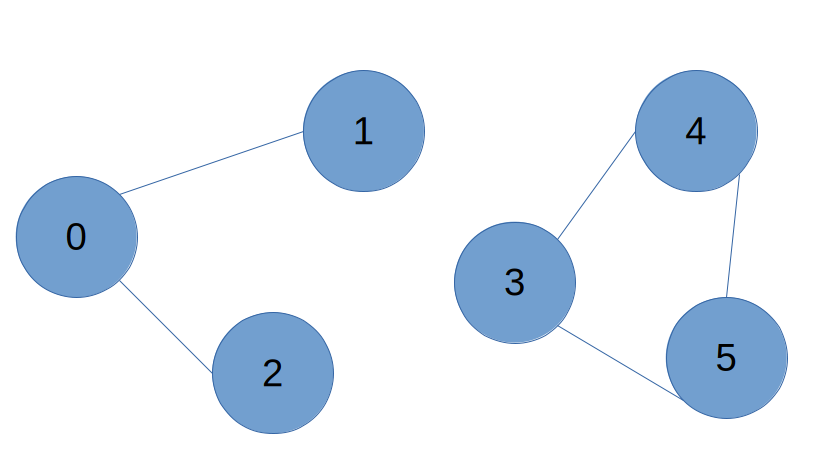
Example 2:
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.
Constraints:
1 <= n <= 2 * 105
0 <= edges.length <= 2 * 105
edges[i].length == 2
0 <= ui, vi <= n - 1
ui != vi
0 <= source, destination <= n - 1
There are no duplicate edges.
There are no self edges.
Solution
Idea
The approach to solving this problem is as follows: We begin at our source vertex and then explore its near vertices (those directly connected to our starting point). Upon reaching a new vertex, we check if it is the destination vertex. If it is, we have found a valid path. If not, we repeat the process, now considering the current vertex as our new starting point. However, this approach has a potential issue: we might revisit vertices we’ve already explored. Therefore, we need to keep track of visited vertices. Consequently, when choosing the next vertex to visit, it should be a neighbor that has not been visited yet. Ultimately, if we exhaust all possibilities without finding the destination, then no valid path exists from the source to the destination, and the answer is False.
Implementation
The graph doesn’t exist directly; instead, we are given a description. Therefore, we need to build a hash map where each vertex corresponds to graph[k]. Since the graph is bidirectional, each edge provides information to populate the connections between two vertices.
Additionally, a set of visited vertices can be maintained to track those already explored.
Now, for the core of the solution: examine the current vertex. If it is the destination, stop and return the positive result. Otherwise, add the current vertex to the set of visited vertices and continue searching for its neighbors. If all reachable vertices have been visited and the destination has not been found, then the result is False.
This approach of exploring as deeply as possible from each vertex is known as Depth-First Search (DFS). Tracking visited vertices is crucial to avoid cycles, which could lead to infinite recursion and prevent the time complexity from being linear.
class Solution:
def validPath(
self, n: int, edges: List[List[int]], source: int, destination: int
) -> bool:
from collections import defaultdict
# dfs implementation adapted
def dfs(graph_node) -> bool:
if graph_node == destination:
return True
for neighbour in graph[graph_node]:
if neighbour not in seen:
seen.add(graph_node)
if dfs(neighbour):
# if destination appears deeper in the path then the result is hold by the return
return True
# At this point there is no more neighbours to visit and destination was not found so return False
return False
graph = defaultdict(list)
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
seen = set()
seen.add(source)
return dfs(source)
Final note
Here the dfs structure is adapted to match the problem requirement. But could take another forms, for example the dfs should be applied to all vertexes and the results should be folded. So take in account adapt the idea to the specific requirement.